干货|不同的损失函数会对深度神经网络带来什么样的影响？

二次损失函数会在神经元犯了明显错误的情况下使得网络学习缓慢，而使用交叉熵损失函数则会在明显犯错的时候学的更快。

今天，我们主要来谈谈不同的损失函数会对深度神经网络带来什么样的影响？（可以参考英文文献：http://neuralnetworksanddeeplearning.com/index.html）

首先，我将列出两种重要的损失函数：

（1）二次损失函数

（2）交叉熵损失函数

稍微解释一下交叉熵损失函数：

我们定义a=f(z),f是激活函数，z是某个神经元的输入，即，

对于一个输出非0即1的问题，我们定下交叉熵损失函数如下：

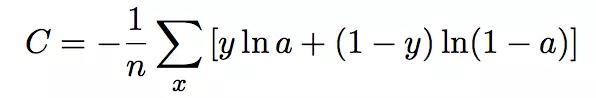
N是训练样本容量，y 是对应样本输出标签，a是样本对应的目标输出。至于为什么这样的一个定义函数能被看作成代价损失函数，这里不予证明。

我们回到二次损失函数，举个例子（单神经元模型），我们期望输入为1时，输出为0；反之，输入为0时，输出为1。首先将权重和偏执初始化为0.6、0.9。刚开始神经元的输出是0.82，如图所示：

然后，我们开始训练这个网络，经过一段时间的学习，得到如下所示：

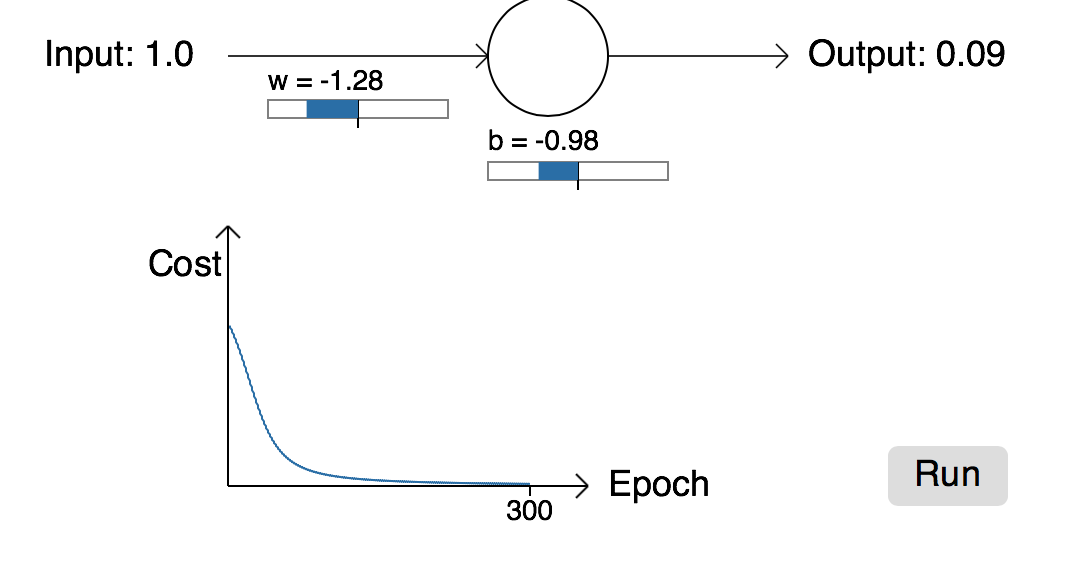
我们看到经过300个epoch后，网络基本能达到我们的学习要求。从图中可以看出：学习曲线起初下降的很快，网络收敛的很快，在大概80epoch左右可以收敛。

但是，如果我们改变权重和偏置的初始值（w=2.00,b=2.00），我们将得到如下的学习曲线：

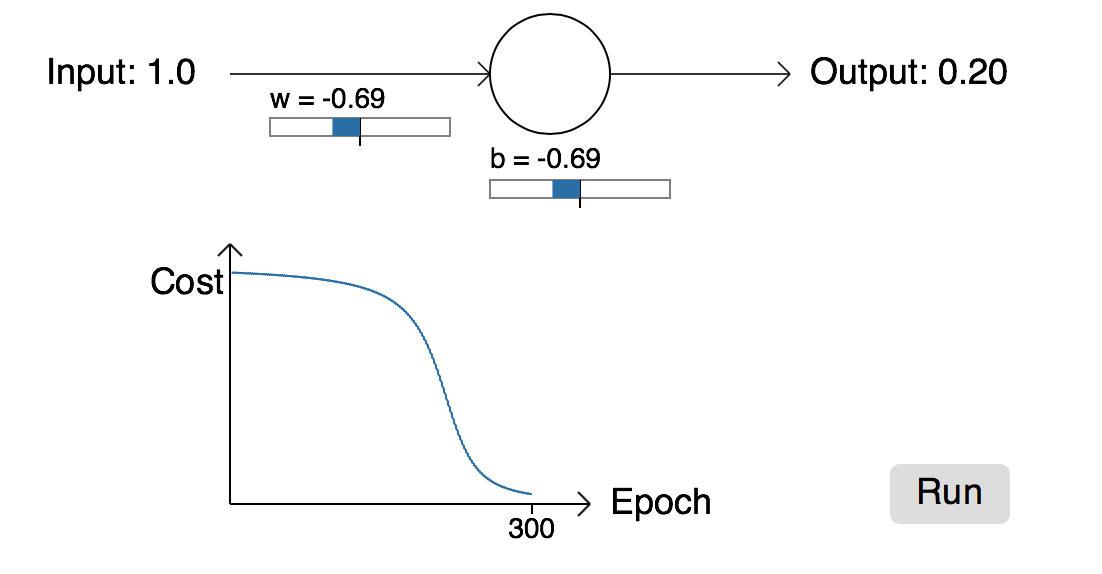
从上图可以看出，网络在300epoch同样达到收敛，但是曲线在起初的时候，学习的很缓慢，几乎没有什么学习能力。同时，我们可以明锐的观察到起初学的很慢时，其对应的cost同样处于很大的一个值，这就会引入我们深思，明明误差很大，为什么还要学习的那么慢。打个比方，你在学习投篮时，第一次投，发现球与篮筐偏的很离谱，下一步，你很快就知道如何调整方向，并且大概知道需要调整多少角度，而在你投的时候，你也会根据上次的偏差调整好适当的角度以达到一个满意的结果。

其实，这就是人的学习能力，就是在你犯了很大错误的时候，你的调整能力是最强的，而上面的二次损失函数似乎表现的差强人意。

那么，为什么人工神经网络中会出现这样的情况呢？也就是为什么人工神经元在其犯很大错误的情况下，反而学习的更加缓慢？

我们还是从数学的角度来分析这个问题，我们知道我们的输入依赖于输入、权重以及偏置。我们真正学习的是那些“权重系数”，这才是“特征”。输入是一定的，关键在于权重系数。权重系数初始化后，由《深度学习之c++实现反向传播算法》知道其更新的变化依赖于损失函数的偏导数。我们说曲线学的很平坦，学习缓慢时，实际上反映出来的结果就是这些对于权重系数的偏导数很小。那么，为什么这些偏导数会变得如此的小以至于网络收敛很慢呢？

我们知道二次代价函数定义如下：

a是输出，y 是目标标签值。

由链式求导法则得到：

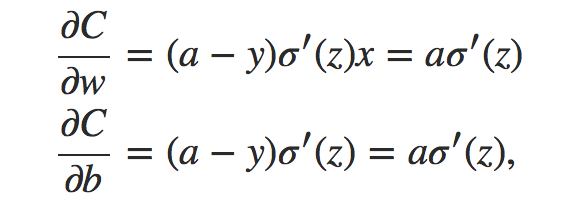
下面给出激活函数是sigmod的曲线及其导函数曲线图：

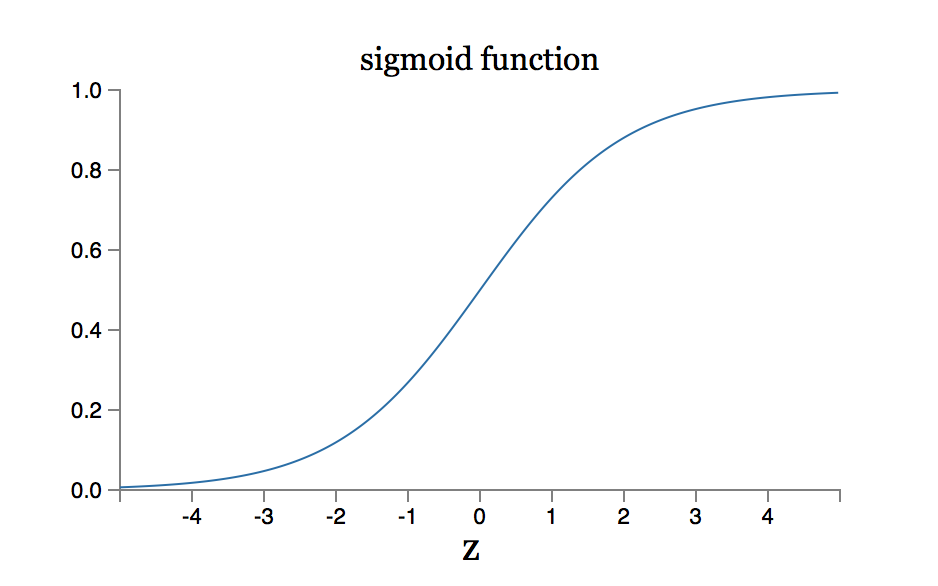
sigmod函数曲线图

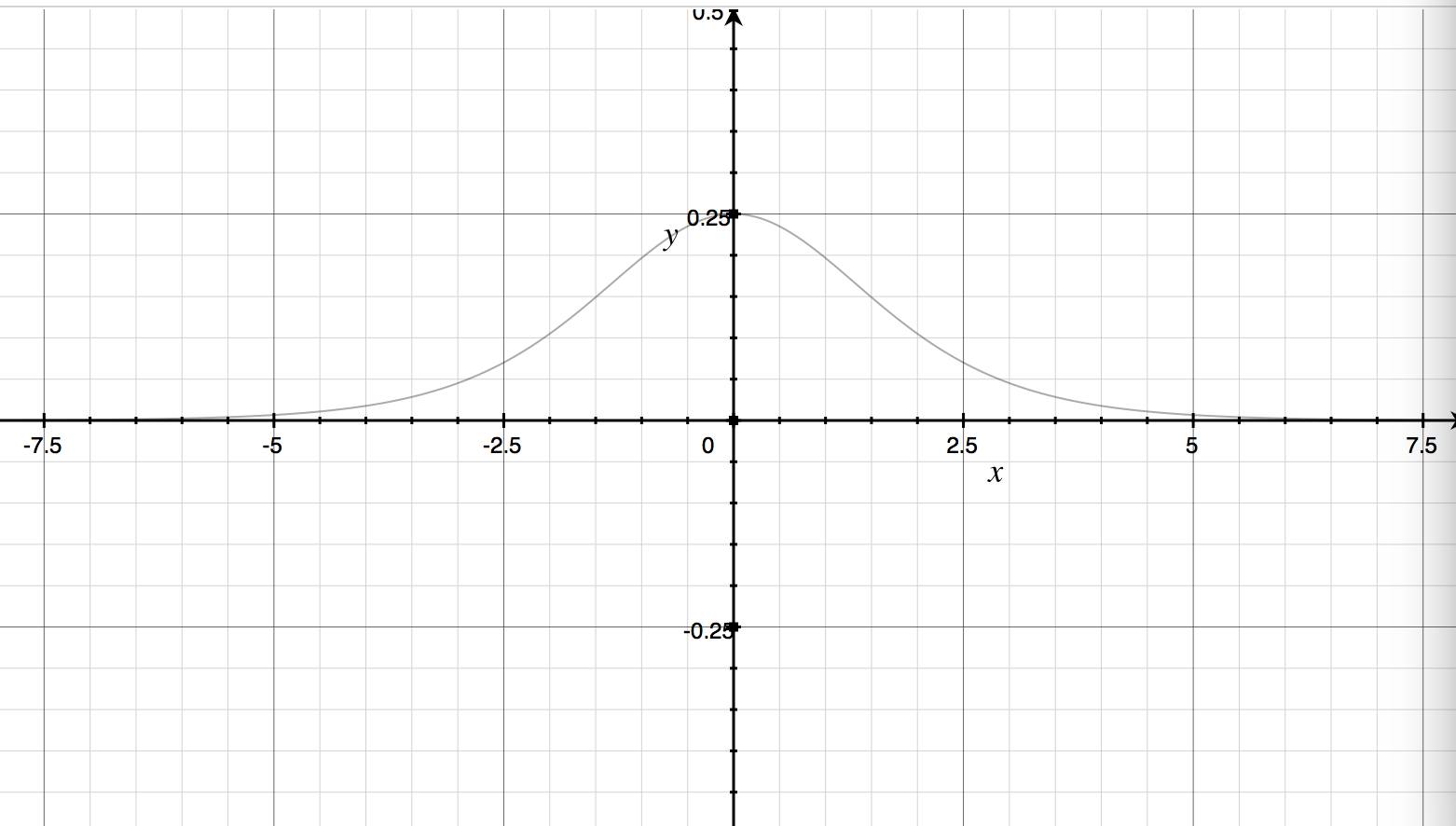
sigmod导函数曲线。

显然，当神经元输出接近1或者0的时候，曲线相当平坦，对应是其导函数曲线值很小，最大导数值是0.25，实际上就是深度神经网络进入了《如何优雅地对深度神经网络进行训练》文中所说的饱和状态了，学习相当缓慢。

引入交叉熵损失函数带来的变化

同样地，由链式求导法则得到：

进一步计算便得到：

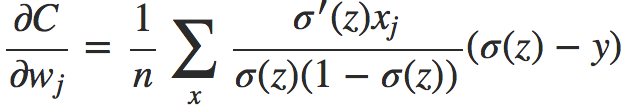
对于激活函数是sigmod的情况，我们可以得到更简洁的形式（σ′(z) = σ(z)(1 − σ(z))）：

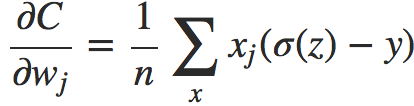
这是一个令人兴奋的表达式，优雅而富有深意。让我们注意一下这个式子中最为关键的一项σ(z)−y ，它其实是告诉我们学习的误差越大，你得到的导数值越大，曲线下降的越快，你的学习速度更快，网络收敛的更快。而且损失对于权重系数的偏导师只与误差有关，且激活函数的导数值无关（还记得那个最大值0.25嘛？）。此时，你可以感叹一下：交叉熵损失函数真的很好。对于初始值w=2.0,b=2.0的那个例子，利用交叉熵损失函数得到的学习曲线如下：

这里，网络收敛的很快，解决了学习缓慢的问题，而且相比于二次损失函数，其收敛速度更快。

结论：不同的损失函数的选择带来的学习效率的不同，二次损失函数会在神经元犯了明显错误的情况下使得网络学习缓慢，而使用交叉熵损失函数则会在明显犯错的时候学的更快。

本文转自全球人工智能，作者徐鹏。

最后，记得关注微信公众号：镁客网（im2maker），更多干货在等你！